In 1933, 23-year-old Hungarian mathematician Esther Klein had an idea. Take any five points and assume no three of them form a line. Will it be always possible to draw a convex quadrilateral from four of the five?

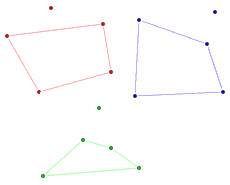
It seems logical, but mathematicians need proof. So Esther's friends Georgy Szekeres and previously-profiled Paul Erdos started to work on it, and cracked it in only(?) two years. Erdos called it the "Happy Ending Problem"... because working on it led to Klein and Szekeres falling in love and getting married. Awwwwwwwwwwwwww.

Szekeres and Erdos then took it up a notch: how many points do you need for a convex pentagon? (Nine) What about a hexagon? What about a n-gon? (That's a polygon with n sides.) The answer is supposedly 2^n-2 + 1, but no one has proven that as of yet.

Szekeres kept chugging at it, proving that a hexagon can be solved in 17 points. He had to use a computer to do it (imagine that in 1933!), running through every possible combination of 17 points on a plane. The proof was published in 2006, a year after he passed away. He and Esther died within an hour of each other; she was 95, he 94.

We wouldn't exactly call it a "happy" ending, but it's as close as two can get...